Лекция 9. Функция Грина. Примеры

В этой лекции мы будем рассматривать уравнение Лапласа в ограниченных областях D, расположенных на плоскости или в пространстве. Точки Р(х, у) и Р_o (х_o , у_o ) на плоскости (или Р(х, у, z) и Р_o (х_o , у_o , z_o ) в пространстве) принадлежат области D и
(или
) - расстояние между точками Р_o и Р.
Предположим, что на границе области D задано нулевое условие Дирихле.

Функция G(P,P_o) называется функцией Грина задачи Дирихле в области D, если для любой фиксированной точки она, как функция от Р , удовлетворяет следующим условиям:

(i) непрерывная в всюду, кроме точки P_o, и G(P,P_o ) = 0 на границе D;
(ii) гармоническая в D за исключением точки P_o;
(iii) в случае плоскости остается гармонической функцией в точке P_o; в случае пространства функция остается гармонической в точке P_o.

Как следует из определения, функция Грина непрерывна и гармонична всюду в области D за исключением точки P_o, в которой она имеет особенность типа в плоскости или в пространстве. Функцию Грина иногда называют функцией источника.

Функция Грина G(P,P_o) (если она существует) однозначно определяется свойствами (i)-(iii). Кроме того, G(P,P_o)>0 в области D. Рассмотрим, к примеру, плоскую область D. Для того, чтобы доказать единственность функции Грина, предположим противное: пусть G₁, и G₂ - две функции, обладающие свойствами (i)-(iii) для заданных области D и точки . Тогда ( G₁ — G₂ ) остается гармонической в любой точке области D, включая и точку P_o, поскольку вблизи точки P_o можно записать

(41)

Каждая скобка в правой части (41) представляет собой функцию, гармоническую всюду в D (см. свойство (iii)), поэтому и разность ( G₁ — G₂ ) - функция гармоническая всюду в D. Кроме того, на границе D функция Следовательно, по принципу максимума в области D.

Далее, если D₁ - часть области D, находящаяся вне малой окрестности точки P_o, то, согласно условиям (i)-(iii), функция G непрерывна в гармонична в D₁, и на границе D₁ принимает неотрицательные значения (так как при ). Поэтому по принципу максимума в D₁ причем нулевое значение внутри области D₁ функция принимать не может. Это означает, что всюду в D.

Пример 1. На плоскости рассмотрим круг радиуса R с центром в начале координат. Построим функцию Грина в круге. При построении этой функции нам понадобится понятие сопряженных точек. Точки P_o и Р^* называются сопряженными относительно окружности, если они лежат на одном луче, исходящем из центра O окружности, и произведение их расстояний от центра равно квадрату радиуса: (см. рис.16).

Рис. 16

Обозначим через r_o =|OP_o| и r^* =|OP^*|. Тогда r_o r^*=R². Так как точки P_o и Р лежат на одном луче, выходящем из начала координат, то

Возьмем функцию

(42)

где r =|P_oP|, r₁ =|PP^*| (см. рис.17). Проверим, что она является функцией Грина для круга.

По теореме косинусов и , где ρ=|OP|.

Рис. 17
Воспользовавшись равенством r_o r^*=R², получим

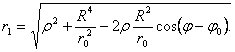Таким образом, величины r и r₁ выражаются через R, ρ, r_o, φ, φ_o, и, в конечном счете, через R, x, y, x_o, y_o. Покажем, что функция G(P,P_o) удовлетворяет пунктам (i)-(iii) определения. Очевидно, что функция непрерывна всюду в замкнутом круге кроме точки Р_о (когда r = 0). На границе круга расстояние ρ=R и, следовательно,

Отсюда Функция G(P,P_o) состоит из двух слагаемых. Первое слагаемое-фундаментальное решение уравнения Лапласа и,следовательно, гармоническая функция всюду, кроме точки P_o.Функция является гармонической всюду в области D , так как точка Р принадлежит области, а точка Р^* лежит вне области D и, следовательно, r₁ >0. Гармоничность этой функции легко проверяется, если записать оператор Лапласа в полярной системе координат с полюсом в точке Р^* (см.аналогичную формулу (33*) с полюсом в точке О):

Поэтому функция G(P,P_o) гармоническая в области D всюду, кроме точки Р_о, а разность G(P,P_o) - ln(1/r) — гармоническая и в точке Р_о.

Аналогично строится функция Грина для шара радиуса R. Она имеет вид где r=|P_oP| , r₁=|PP^*| , r_o=|OP_o|. Точка P^*(x^* , y^* , z^*) сопряженная точке Р_o (х_o , у_o , z_o ) относительно сферы радиуса R с центром в точке О, то есть . Координаты x^* , y^* , z^* вычисляются по формулам:

Пример 2. Функцию Грина можно рассматривать не только для ограниченных, но и для неограниченных областей. В качестве примера построим функцию Грина для полуплоскости. Для этого определим точки, сопряженные относительно прямой: точки Р_о и Р^* называются сопряженными относительно прямой, если они симметричны относительно этой прямой (см. рис.18).

Рис. 18 Рис. 19

Функция где
,
(см. рис.19), удовлетворяет свойствам (i)-(iii) в полуплоскости у > 0. В самом деле, на границе области при у = 0 расстояние r = r₁, поэтому Гармоничность функции всюду в области у > 0 проверяется непосредственно вычислением частных производных:

Поэтому

Следовательно, функция G(P,P_o) гармоническая в области у > 0 всюду, кроме точки Р_о, а разность G(P,P_o) - ln(1/r) гармоническая и в точке Р_о.

Для полупространства z > 0 функция Грина имеет вид где