Лекция 8. Принцип максимума для гармонических функций

Среди свойств, которыми обладают гармонические функции, одно свойство, называемое принципом максимума, несомненно имеет ведущее значение.

Теорема. Если функция U=U(x,y) гармоническая в ограниченной области D и непрерывная в соответствующей замкнутой области то она не может внутри этой области принимать значения, большие чем максимум ее значений на границе Г, и меньшие, чем минимум ее значений на Г, то есть

(39)

Доказательство. Обозначим через m максимум значений U(x,y) на Г и предположим, что максимальное значение функции равно U(x_o,y_o)=M>m и принимается во внутренней точке (x_o , y_o) области D. Составим вспомогательную функцию

где d - диаметр области D (максимальное расстояние между любыми двумя точками, принадлежащими области). Из неравенства

вытекает, что на Г

В то же время функция V(x,y) принимает свое максимальное значение в некоторой (внутренней) точке области D, причем

Как известно, в этой точке V_x = V_y = 0, а следовательно, Однако

Полученное противоречие означает, что предположение M > m неверно, и мы доказали, что внутри D

Для доказательства неравенства, ограничивающего U(x, y) снизу

достаточно применить уже полученный результат к функции - U(x, y), которая, очевидно, тоже является гармонической. Теорема о максимуме и минимуме доказана.

На самом деле, если гармоническая функция , то она не может принимать внутри области D значения, равные и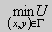, то есть

Это утверждение называется строгим принципом максимума (в отличие от предыдущего утверждения - "нестрогого" принципа максимума). Его доказательство сложнее, и мы доказывать это утверждение не будем. Сформулируем следствия из него.

Следствие 1. Если функция U=U(x, y) непрерывная в ограниченной замкнутой области и гармоническая в D, то

(40)

В частности, если , то U(x, y) ≡ 0 в D.

Это утверждение вытекает из (39):

Объединяя эти неравенства в систему, будем иметь:

Из принципа максимума следуют и многие другие важные свойства гармонических функций. Однако мы сейчас сформулируем и докажем лишь две теоремы.

Напомним постановку задачи Дирихле: в области D найти решение уравнения Лапласа, удовлетворяющее граничному условию U|_Г = f(s).

Теорема о единственности решения задачи Дирихле.

Решение задачи Дирихле для уравнения Лапласа в ограниченной области (если оно существует) единственное.

Доказательство. Пусть задача имеет два решения U=U₁(x, y) и U=U₂(x, y), удовлетворяющих одному и тому же условию Дирихле на границе Г. Тогда их разность V = U₁ - U₂ тоже будет непрерывной и гармонической функцией и на границе будет обращаться в нуль. По принципу максимума

Следовательно, V = U₁ - U₂ ≡ 0, то есть U₁(x, y) ≡ U₂(x, y). Единственность доказана. Вторая теорема имеет еще более длинное название.

Теорема о непрерывной зависимости решения задачи Дирихле от граничных условий.

Пусть U₁ и U₂ - две гармонические в области D функции, граничные значения которых равны, соответственно, f₁(s) и f₂(s), Если при некотором то всюду в рассматриваемой области D.

Доказательство. Рассмотрим функцию V = U₁ - U₂, удовлетворяющую уравнению Лапласа в области D и принимающую на границе Г значения f(s) = f₁(s)-f₂(s). На основании следствия 1 мы можем утверждать, что

что и требовалось доказать.

Эти теоремы имеют большое значение в вопросе о корректности задачи Дирихле, который мы рассмотрим в дальнейшем.

Отметим, что принцип максимума выполняется и для функций, гармонических в пространственных областях.