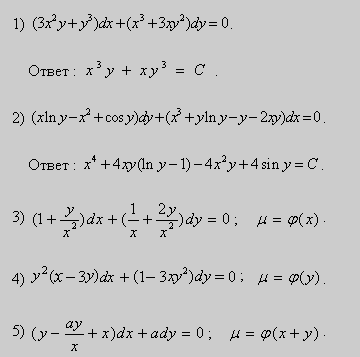Лекция 2. Дифференциальные уравнения первого порядка, не разрешённые относительно производной .

Рассмотрим уравнение вида

F ( x , y , y ' ) = 0 ,

не разрешённое относительно производной. Если попытаться выразить из него y ' , то можно получить , вообще говоря , несколько уравнений

Геометрически это означает , что в каждой точке задаётся несколько направлений поля (см.рис.2).

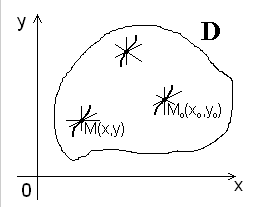
Рис. 2

Следовательно через любую точку M ( x , y ) может проходить несколько интегральных кривых . Для того, чтобы выделить из этого множества единственную интегральную кривую, проходящую через заданную точку M₀ ( x₀ , y₀) , надо помимо значений ( x₀, y₀) дополнительно задать в этой точке направление поля y ' ( x₀) = y '_{0 .}

Задача Коши . Найти решение уравнения F ( x, y, y ' ) = 0, удовлетворяющее начальным условиям y ( x₀) = y₀ и y ' ( x₀) = y '₀, где y '₀ - решение уравнения F ( x₀, y₀, y ' ) = 0.

Теорема существования и единственности решения задачи Коши.

Пусть в некоторой окрестности U точки (x₀, y₀, y '₀), где y '₀ - решение уравнения F ( x₀, y₀, y ' ) = 0, выполнены условия :

1) F( x , y , y ' ) определена, непрерывна и имеет непрерывные частные производные F'_y и F'_y ' по совокупности переменных ( x , y , y ' ) ;

2) значение производной F_y'_' (x₀, y₀, y'₀)0.

Тогда в некоторой окрестности точки x₀ существует единственное решение уравнения F (x, y, y') = 0, удовлетворяющее условиям y(x₀) = y₀ и y' (x₀) = y'₀.

Метод введения параметра.

На практике при решении уравнений F( x , y , y ' ) = 0 часто используют следующий метод.

Предположим , что уравнение F( x , y , y ' ) = 0 “легко” решить относительно y : y = f ( x , y ' ). Тогда введем замену y ' = p ( параметр зависит от x ). Предполагая, что дифференциальное уравнение имеет решение y = y ( x ) , получим ( в силу уравнения )

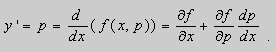
Из этих равенств выражаем :

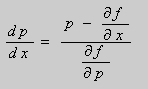
Это уравнение разрешено относительно производной . Пусть его общее решение имеет вид p = p ( x , C ) .Тогда общее решение заданного уравнения можно записать в виде y =f ( x , p ( x , C ) ). Решение найдено.

Таким методом можно решать , в частности , уравнения Лагранжа и Клеро.

Уравнение вида называется уравнением Лагранжа. Оно является линейным относительно переменных x и y . Частным случаем этого уравнения является уравнение Клеро. Оно имеет вид :

Пример 1 . Решить уравнение

(5)

Решение. Выразим из уравнения (5) переменную y :

.Заменим и получим

(6)

Продифференцируем его по x :

Из этих равенств получаем :

или

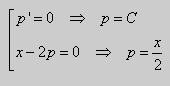
После подстановки этих выражений в (6) будем иметь

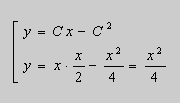
Ответ :

Этим методом можно также решать уравнения , в которых "легко" выражается переменная x . Рассмотрим

Пример 2 . Решить уравнение

(7)

Решение . Выразим из уравнения (7) переменную x и введём параметр p :

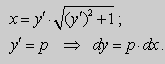
Получим

(8)

Продифференцируем уравнение (8) по p :

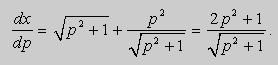
Отсюда в силу равенства dy = p dx получим :

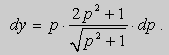
Проинтегрируем это уравнение :

Таким образом , с учётом ( 8 ) , получаем общее решение в параметрическом виде :

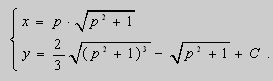
Примеры. Решить уравнения :

Уравнения в полных дифференциалах.

Рассмотрим уравнение

(9)

Если в уравнении (9) функции

то мы имеем

В этом случае уравнение (9) называют уравнением в полных дифференциалах. После интегрирования получим общее решение уравнения

U (x , y) = C

Теорема 1. Пусть функции непрерывные в некоторой односвязной области . Тогда необходимым и достаточным условием того, что уравнение (9) - в полных дифференциалах , является условие

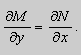
Доказательство. 1. Необходимость.

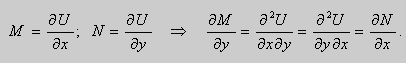
2. Достаточность.

Рассмотрим функцию

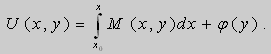
Тогда

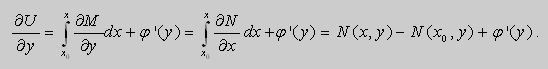
Если выбрать функцию так, чтобы

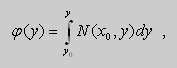
то и , следовательно ,

Таким образом , в уравнении (9)

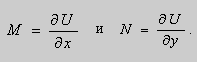
Теорема 1 доказана.

Из теоремы следует , что общее решение уравнения (9) можно записать в виде

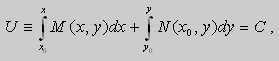
если 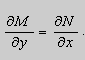Функцию U можно также представить в виде

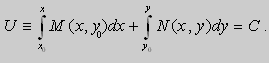
Предположим , что 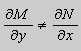. Тогда можно попытаться найти такую функцию , чтобы . Функция называется интегрирующим множителем . В этом случае мы получаем уравнение

в полных дифференциалах. Следовательно, в силу теоремы 1,

Это уравнение позволяет найти интегрирующий множитель. Рассмотрим

Пример. Решить уравнение

(10)

Решение. Простой проверкой убеждаемся , что (10) не является уравнением в полных дифференциалах. Умножим его на неизвестную функцию :

Попробуем найти из уравнения :

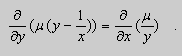
или

(11)

Пусть . Обозначим через и получим

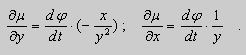
После подстановки этих выражений в (11) будем иметь :

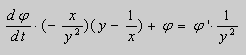
или

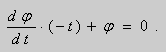
Проинтегрируем полученное уравнение :

Таким образом, интегрирующий множитель можно взять в виде

Умножим теперь уравнение (10) на функцию

или

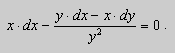
Отсюда

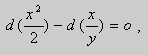
или

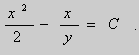
Теорема 2. Если функции M и N непрерывные , имеют непрерывные частные производные первого порядка по x и по y , и , то интегрирующий множитель существует.

Замечание. Точка ( x₀, y₀ ), в которой M ( x₀, y₀) = N ( x₀ , y₀) = 0 является особой точкой уравнения (9). Поведение решений в окрестности особой точки изучается в лекции 3.

Примеры. Решить дифференциальные уравнения :