|
Московский Государственный Строительный Университет Арефьев В.Н. Лекции по "Уравнениям математической физики" |
|
|
Московский Государственный Строительный Университет Арефьев В.Н. Лекции по "Уравнениям математической физики" |
|
В этой лекции рассматривается задача Коши для уравнения первого порядка y' = f (x , y): найти решение y = y (x)уравнения, удовлетворяющее начальному условию y (x0) = y0 .
Вначале напомним некоторые вспомогательные понятия и утверждения.
1. Равномерная сходимость последовательности :
2. Свойства равномерно сходящихся последовательностей функций :
y ( x ) 
y ( x ) - непрерывная в [a , b ] ;
б) функции yn( x ) - непрерывные в [a , b] , yn( x ) y ( x ) 
;
y ( x0) при x0
( a , b ) , y 'n( x ) 
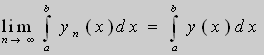(x ) yn( x ) y ( x ) , y' ( x ) = (x ) в (a , b ) .
3. Теорема Вейерштрасса : ряд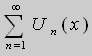 
определён в
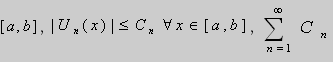- сходится
4. Условие Липшица : функция f ( x , y ) в области G удовлетворяет условию Липшица по y
5. Лемма : функция f(x, y) - непрерывная по x и удовлетворяет условию Липшица по y в области G, следовательно f ( x , y ) непрерывная в G по совокупности x и y .
Пусть G - ограниченная замкнутая область на плоскости ( x , y ). Точка ( x0, y0) G. Пусть f ( x , y ) - непрерывна в G и удовлетворяет условию Липшица по y . Тогда существует единственное решение y = y ( x ) уравнения y' = f (x , y ), удовлетворяющее начальному условию y ( x0) = y0 . Функция y(x) определена и непрерывна в некоторой окрестности 
, и имеет там непрерывную производную.
Доказательство.
Шаг 1.
Лемма. Если f ( x , y ) - непрерывная в G , то задача Коши равносильна интегральному уравнению
 |
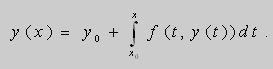(1) |
В самом деле , если y ( x ) - решение задачи Коши в окрестности 
выполняется тождество
Следовательно,
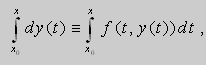
т.е.
 |
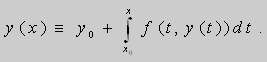(2) |
Обратно, если y ( x ) - непрерывное решение интегрального уравнения (1) , причём 
, то справедливо тождество (2). Так как f ( x , y ) - непрерывная функция в G , то по теореме Барроу y ( x ) - дифференцируемая и удовлетворяет тождеству
Шаг 2.
Построим функции yn(x) - последовательные приближения к решению интегрального уравнения (1). В силу непрерывности функции f ( x , y ) имеем 
. Рассмотрим две прямые : 
и возьмём на оси OX отрезок [a , b] такой, как указано на рис. 1.
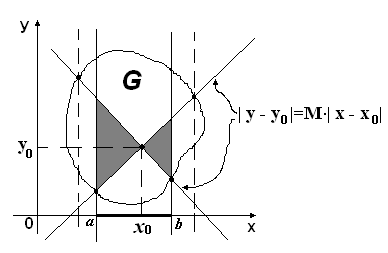
а) В качестве начального приближения возьмём, к примеру, функцию 
.
б) Следующее приближение построим по формуле
И так далее.
в) Пусть
 |
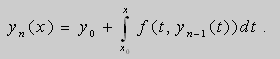(3) |
Каждая из функций yn(x) (n=0,1,2,...) удовлетворяет следующим условиям :
1) yn(x0) = y0 .
2) yn(x) определена на [a , b ], так как выполняется неравенство
 |
(4) |
Это неравенство означает, что yn( x ) может пересекать только боковые стороны заштрихованных треугольников (см. рис.1).
3) yn( x ) - непрерывно дифференцируемая функция на [a , b ].
Шаг 3.
Докажем , что yn( x ) y ( x ) в некотором интервале 
.
Рассмотрим тождество
В правой части этого тождества записана n-ая частичная сумма ряда
Так как этот ряд мажорируется некотоым сходящимся числовым рядом, то по теореме Вейерштрасса он сходится равномерно к непрерывной функции y( x ).
В самом деле ,
(эта оценка следует из (4)).
Далее
Воспользуемся условием Липшица и получим
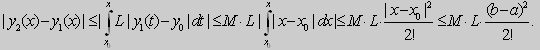
По индукции для любого 
будем иметь
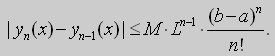
Следовательно в качестве мажорирующего ряда можно взять
Шаг 4.
Перейдём к пределу в равенстве (3) при 
и получим
или
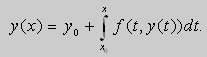
Законность этого предельного перехода под знаком интеграла можно обосновать с помощью свойств равномерно сходящихся последовательностей. Однако это можно проверить и непосредственно :
Используя условие Липшица и равномерную сходимость функций yn( x ), эту оценку можно продолжить
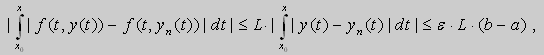
где
- любое положительное, наперёд заданное число.
Шаг 5.
Докажем , что решение y (x) - единственное. Пусть 
- какое-либо другое решение интегрального уравнения (1). Тогда
Таким образом,
Если предположить, что 
, то будем иметь
Замечание. Метод последовательных приближений, рассмотренный на 2-ом шаге, является одним из основных приближённых методов решения задачи Коши. Иногда его называют также методом Пикара.
