Лекция 3. Исследование особых точек .

Рассмотрим уравнение

(12)

Если функции M и N непрерывные в некоторой области и в точке значение , то данное уравнение равносильно уравнению

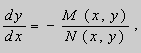
решения которого являются функциями от x. Аналогично, если , то уравнение (12) равносильно уравнению

у которого решения - функции от y.

В том случае, когда , точка - является особой точкой. Рассмотрим

Примеры. 1. В уравнении

точка ( 0 , 0 ) – особая. Решим его :

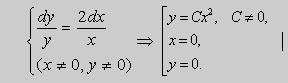- решения этого уравнения.

Интегральные кривые изображены на рис.3. В этом случае точка (0,0) называется узлом.

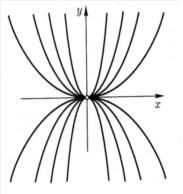
Рис. 3

2. В уравнении

точка ( 0 , 0 ) – также особая. Его решения имеют вид :

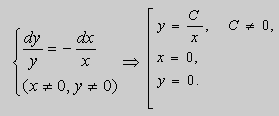
Интегральные кривые изображены на рис. 4. Такая особая точка называется седлом.

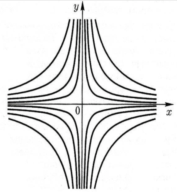
Рис. 4

3. В уравнении

общее решение может быть записано в виде

Интегральные кривые – окружности (см. рис. 5) , а особая точка (0,0) называется центром.

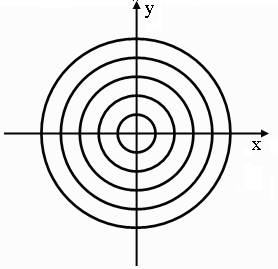
Рис. 5

4. Уравнение

является однородным уравнением. Его решения могут быть записаны в виде

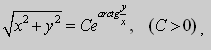
или в полярных координатах

Интегральные кривые представляют собой логарифмические спирали ( см. рис. 6 ) , а особая точка ( 0 , 0 ) называется фокусом.

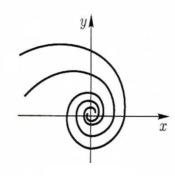
Рис. 6

Особые точки уравнения (12) тесным образом связаны с точками покоя системы двух уравнений вида

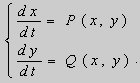
Рассмотрим простейший случай, когда функции P ( x , y ) и Q ( x , y ) – линейные :

(13)

причем определитель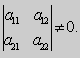

У этой системы точка ( 0 , 0 ) является точкой покоя. От системы (13) , исключая переменную t , можно перейти к уравнению

(14)

решения которого определяют фазовые траектории на плоскости ( x , y ). При этом точка ( 0 , 0 ) является особой точкой уравнения (14). Таким образом , исследование точки покоя системы (13) можно свести к исследованию особой точки уравнения (14) , и наоборот, изучив точку покоя системы (13) , можно определить тип особой точки уравнения (14). При исследовании точки покоя системы (13) составляют характеристическое уравнение

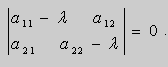
Рассмотрим следующие случаи :

1. Корни характеристического уравнения действительные, различные, одинакового знака В этом случае точка ( 0 , 0 ) – узел, а траектории в окрестности этой точки изображены на рис. 7.

Рис. 7

Рис. 8

2. Корни характеристического уравнения действительные, различные, разного знака. В этом случае точка ( 0 , 0 )– седло ( см. рис. 8 ).

3. Корни характеристического уравнения комплексные : q ≠ 0. Если p ≠ 0 ,то точка ( 0 , 0 ) - фокус ( см. рис.9 ).

Если p = 0 , то точка ( 0 , 0 ) – центр ( см. рис. 10 ).

Рис. 9

Рис. 10

4.Характеристическое уравнение имеет кратный корень : . В этом случае может быть либо вырожденный узел ( см. рис. 11 ) , либо дикритический узел ( см. рис. 12 ).

Рис. 11

Рис. 12