Лекция 6. Метод Даламбера

В этой лекции решение задачи Коши для волнового уравнения

(23)

проведем методом Даламбера. При этом процесс решения разобьем на несколько шагов.

Шаг 1. Заменим переменные (x, t) новыми переменными (ξ,η), в которых волновое уравнение примет другой вид: Такая замена выполняется по формулам

(24)

Проверим это:

После подстановки этих производных в волновое уравнение, получим:

что и требовалось доказать.

Шаг 2. Преобразованное уравнение легко решается двумя последовательными интегрированиями (сначала по переменной η , а затем по ξ):

где C₁(η) – произвольная функция от η. Так как C(ξ) – произвольная функция, то и

– также произвольная функция.

Окончательно, общее решение U(ξ,η) имеет вид

(25)

где C₁(η) и C₂(ξ) – произвольные функции.

Шаг 3. Для нахождения общего решения первоначального уравнения подставим в (25) вместо ξ и η выражения (24):

(26)

Шаг 4. Определим функции C₁ и C₂, используя начальные условия из (23). После подстановки первого условия получим

Найдем производную функции U в (26) по переменной t и подставим второе условие:

В результате будем иметь систему уравнений

(27)

Если проинтегрировать второе уравнение системы (27) по x в пределах от x_o до х , то получим следующую систему:

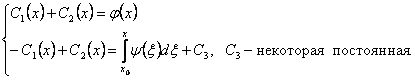
При сложении этих уравнений получим

Если из первого уравнения системы вычесть второе уравнение, то будем иметь

Подставим теперь полученные функции в общее решение (26):

(28)

Поменяем местами пределы интегрирования во втором интеграле, стоящем в скобках в (28). В результате получим решение исходной задачи Коши

(29)

Формула (29) называется формулой Даламбера.

Далее мы исследуем решение, определяемое по формуле Даламбера.

Пространственно-временная интерпретация формулы Даламбера

При исследовании формулы Даламбера будем исходить из физического смысла волнового уравнения. Рассмотрим уравнение свободных колебаний бесконечной струны

(30)

и начальные условия

(31)

Такая задача Коши с помощью замены независимой переменной сводится к задаче (23):

Решение преобразованной задачи имеет вид (см. формулу Даламбера (29):

Если теперь в эту формулу вместо τ подставить at, то получится решение исходной задачи

(32)

Прежде, чем перейти к физической интерпретации этой формулы, сделаем следующее замечание.

Замечание. Рассмотрим в отдельности функции C₁(x-at) и C₂(x-at), входящие в общее решение (26) (коэффициент а в них появился потому, что нас сейчас интересует более общее уравнение (30)). Начнем с функции C₁(x-at) и построим графики этой функции при возрастающих значениях t: t=t_o, t=t₁, t=t₂ и т.д. (см. рис. 8).

Рис. 8

Если по очереди проецировать эти картинки на экран (как в мультфильмах), то они «побегут» вправо. Процесс передвижения отклонения по струне называется волной. При этом коэффициент а является скоростью распространения волны. В самом деле, предположим, что параллельно оси х движется наблюдатель со скоростью а. Пусть в некоторый момент t_o он находился в точке x_o. Тогда за промежуток наблюдатель сместится вправо на величину и окажется в точке Если в точке x_o наблюдатель видел отклонение струны на величину то в момент t величина отклонения – будет точно такой же! То есть наблюдатель будет видеть форму струны не изменяющейся.

Вторая функция C₂(x-at) тоже представляет собой волну, но только она будет распространяться со скоростью а влево. Часто функции C₁(x-at) и C₂(x-at) называют, соответственно, прямой и обратной волной. Таким образом, общее решение U(x,t) (формула (26)) волнового уравнения является суперпозицией прямой и обратной волны.

Теперь дадим интерпретацию формулы Даламбера для двух частных случаев.

СЛУЧАЙ 1. Предположим, что начальное отклонение отлично от нуля, а начальная скорость равна нулю. Это означает, что начальные условия имеют вид

При таких начальных условиях получается решение задачи Коши, которое называется волной отклонения. Уравнение волны отклонения определяется формулой Даламбера

то есть решение U в некоторой точке x_o в момент времени t_o зависит от значений начальной функции φ в двух точках на оси х: в точке (x_o - at_o) и в точке (x_o + at_o) (см. рис. 9).

Рис. 9

Значение U равно среднему арифметическому значений начальной функции φ в точках (x_o - at_o) и (x_o + at_o). На рис. 9 изображена плоскость xOt, которая называется фазовой плоскостью. На оси х указаны точки (x_o - at_o, 0) и (x_o + at_o, 0), в которых начальные отклонения струны определяют величину отклонения струны в точке x_o в момент времени t_o. Эти точки являются точками пересечения прямых x - at = x_o - at_o и x + at = x_o + at_o с осью х. Указанные прямые называются характеристиками волнового уравнения. Треугольник с вершиной в точке (х_o, t_o) и основанием, которое получается при пересечении характеристик с осью х (см. рис. 9), называется характеристическим треугольником.

Используя такую интерпретацию формулы Даламбера, изобразим фазовую картину решения следующей задачи:

Замечание. На самом деле начальные отклонения струны не могут быть разрывными в точках х = -1 и х = 1, ведь струна не разрывается. Однако мы не слишком сильно погрешим против истинной картины распространения колебаний, если будем считать их кусочно постоянными. Дело в том, что, во-первых, рассматриваются очень малые колебания струны, и, во-вторых, малые изменения начальных значений незначительно влияют на решение задачи.

На рисунке 10 изображена фазовая плоскость x0t. Решение U(x,t) задачи отлично от нуля только в заштрихованных областях, причем начальное отклонение распространяется с одинаковой скоростью в двух противоположных направлениях – возникает прямая и обратная волны. Границы этих областей – это характеристики волнового уравнения: x - at = -1, x - at = 1, x + at = -1, x + at = 1.

Рис. 10

Если рассмотреть процесс колебания некоторой фиксированной точки струны x = x_o, то нетрудно заметить, что она колеблется только в конечный промежуток времени: от момента до момента , то есть В остальное время точка x_o находится в покое. Говорят, что в момент t₁ через точку x = x_o проходит передний фронт волны, а в момент t₂ - задний фронт волны. Вообще, фронтом волны называется граница между возмущенной (колеблющейся) и невозмущенной областями среды (точками струны). Для прямой волны уравнение переднего фронта x - at = 1, а заднего фронта x - at = -1. Для обратной волны, соответственно, x + at = -1 - уравнение переднего фронта, а x + at = 1 - заднего фронта.

Рассмотрим теперь

СЛУЧАЙ 2. Пусть начальное отклонение равно нулю, а начальная скорость отлична от нуля. Это означает, что начальные условия имеют вид

В этом случае решение задачи Коши называют волной импульса. Оно имеет вид (см. формулу Даламбера)

то есть решение U в некоторой точке x_o в момент времени t_o зависит от начальных скоростей ψ во всех точках отрезка [x_o - at_o , x_o + at_o] (см. рис 11). Значение U равно (интегральному) среднему значению начальной скорости на отрезке [x_o - at_o , x_o + at_o], умноженному на промежуток времени t.

Рис. 11

На рис. 11 изображена фазовая плоскость x0t. Точки (x_o - at_o, 0) и (x_o + at_o, 0) являются точками пересечения характеристик x - at = x_o - at_o и x + at = x_o + at_o с осью х. В качестве примера приведем фазовую картину решения следующей задачи:

Рис. 12

Рис. 12 описывает процесс колебания струны, которой сообщается начальная единичная скорость на отрезке -1<x<1 . В этом случае вся верхняя половина фазовой плоскости характеристиками разбивается на шесть областей. В каждой из этих областей решение U(x,t) легко находится по формуле Даламбера:

1. В области 1 (так же, как и в области 5) функция

При вычислении интеграла всегда удобно представить себе характеристический треугольник с вершиной в точке, лежащей в соответствующей области (см. рис 12). Тогда значение U(x,t) будет определяться значениями начальной функции ψ(x) в основании характеристического треугольника.

2. В области 2 функция

3. В области 3 функция

4. В области 4 функция

5. В области 6 функция

Это решение в различные моменты времени можно изобразить на плоскости x0U (см. рис 13). Здесь для простоты положим a=1.

Рис. 13

Графики функции U(x,t), изображенные на рис. 13, задают форму струны в различные моменты времени.