Метод характеристик
Распространение волн
Рассмотрим функциюВидно, что функция ![]() представляет собой неизменный профиль
представляет собой неизменный профиль ![]() , перемещающийся вправо в положительном направлении оси
, перемещающийся вправо в положительном направлении оси ![]() с конечной скоростью, равной
с конечной скоростью, равной
![]() . При этом отклонение в точке
. При этом отклонение в точке ![]() повторяет отклонение в точке
повторяет отклонение в точке ![]() лишь со сдвигом по времени на время запаздывания
лишь со сдвигом по времени на время запаздывания ![]() .
.
В подвижной системе координат, движущейся в право со скоростью ![]() , наблюдатель будет видеть все время один и тот же как бызастывший профиль струны.
, наблюдатель будет видеть все время один и тот же как бызастывший профиль струны.
Такой процесс распространения отклонений (возмущений) вструне представляет собой волновой процесс. При этом волну, бегущую с постоянной скоростью
![]() вправо вдоль оси
вправо вдоль оси ![]() назовем прямой бегущей волной.
назовем прямой бегущей волной.
Наглядное изображение такого волнового процесса можно получить, вводя плоскость состояний (фазовую плоскость) ![]() и описывая исследуемый процесс в верхней полуплоскости
и описывая исследуемый процесс в верхней полуплоскости ![]() (рис. 4).
(рис. 4).
Функция ![]() сохраняет постоянные значения на линиях
сохраняет постоянные значения на линиях
![]() плоскости
плоскости ![]() (рис. 5 а),которые являются характеристиками волнового уравнения ( 1).
(рис. 5 а),которые являются характеристиками волнового уравнения ( 1).
Предположим теперь, что функция ![]() отлична от нуля лишь в интервале
отлична от нуля лишь в интервале ![]() и равна нулю вне этого интервала. Функцию такого вида называют финитной, а отрезок
и равна нулю вне этого интервала. Функцию такого вида называют финитной, а отрезок ![]() - носителемэтой финитной функции.
- носителемэтой финитной функции.
Для этого случая на плоскости состояний проведем через точки ![]() и
и
![]() характеристики
характеристики ![]() и
и ![]() . Они разбивают полуплоскость
. Они разбивают полуплоскость ![]() на три области. В области
на три области. В области ![]() функция
функция ![]() отлична от нуля, причем характеристики
отлична от нуля, причем характеристики ![]() и
и
![]() выделяют передний и задний фронтыраспространяющейся направо волны, так как на плоскости состояний они отделяют область возмущений
выделяют передний и задний фронтыраспространяющейся направо волны, так как на плоскости состояний они отделяют область возмущений ![]() от невозмущенных областей
от невозмущенных областей ![]() ,
, ![]() , где функция
, где функция ![]() равна нулю.
равна нулю.
Аналогично функция ![]() представляет собой волну, распространяющуюся с постоянной скоростью
представляет собой волну, распространяющуюся с постоянной скоростью
![]() влево в отрицательном направлении оси
влево в отрицательном направлении оси ![]() . Такую волну назовем обратной бегущей волной. Две характеристики
. Такую волну назовем обратной бегущей волной. Две характеристики ![]() и
и ![]() проходящие через точки
проходящие через точки ![]() и
и ![]() выделяют фронты обратной волны (рис. 5 б).
выделяют фронты обратной волны (рис. 5 б).
| Наверх | К началу | К оглавлению |
Распространение волн отклонения
Пусть в задаче ( 1),( 2) ![]() , т.е. струна колеблется тольков результате начального отклонения, форма которого определяется функцией
, т.е. струна колеблется тольков результате начального отклонения, форма которого определяется функцией ![]() . Решение ( 6) принимает в этомслучае простой вид:
. Решение ( 6) принимает в этомслучае простой вид:
Из предыдущих рассуждений видно, что решение ( 17) задачи ораспространении волн отклонения представляет собой суперпозицию(наложение) прямой и обратной бегущих волн, профиль которых с точностью до множителя, равного ![]() , совпадает с профилемначального распределения отклонений струны.
, совпадает с профилемначального распределения отклонений струны.
Рассмотрим, например, случай, когда
![]() отлична от нуля на интервале
отлична от нуля на интервале ![]() и четна. На рисунке 6 показаны профили струны в различныемоменты времени (Пунктиром показаны прямая и обратнаяволны в области их наложения). В начальный момент временипрофили обеих волн совпадают. До тех пор, пока
и четна. На рисунке 6 показаны профили струны в различныемоменты времени (Пунктиром показаны прямая и обратнаяволны в области их наложения). В начальный момент временипрофили обеих волн совпадают. До тех пор, пока ![]() , есть участок, где волны накладываются друг на друга, начиная с момента
, есть участок, где волны накладываются друг на друга, начиная с момента ![]() эти волныуже не накладываются и расходятся в разные стороны.
эти волныуже не накладываются и расходятся в разные стороны.
Очень наглядное изображение описанного процесса можно получить нафазовой плоскости, если провести на ней характеристики для прямой и обратной волн через точки ![]() и
и ![]() (см. рис 7).
(см. рис 7).
Точки этих характеристик соответствуют положениям переднего изаднего фронтов обеих волн в различные моменты времени.Полуплоскость разбивается ими на 6 частей. Колебание происходиттолько в тех точках и в те моменты времени, которые соответствуютточкам зон I, II и III. В зоне II действует только прямая волна, взоне III - только обратная, а в зоне I и та и другая. В точках,соответствующих зонам IV и V, колебаний еще нет, так как до них недошел передний фронт прямой (зона IV) и обратной (зона V) волн, а вточках, соответствующих зоне VI, колебания уже нет, так как черезних задние фронты обеих волн уже прошли.
| Наверх | К началу | К оглавлению |
Распространение волн импульса
Пусть теперь в задаче Коши ( 1),( 2)Решение Даламбера ( 6) в этом случае запишется в виде
Покажем, что и это решение представляет собой суперпозицию двухбегущих волн, распространяющихся в противоположных направлениях со скоростью
![]() . Для этого введем функцию
. Для этого введем функцию
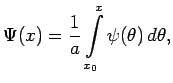
Тогда формуле ( 18) можно придать вид
![$\displaystyle u(x,t)=\frac{1}{2}\left[\Psi(x+at)-\Psi(x-at)\right].$](images/img210.png)
Такая форма решения показывает, что и в случае сообщения частицамструны начального импульса колебания распространяются в виде суперпозиции прямой ![]() и обратной
и обратной ![]() бегущих волн. Форма первой из них в начальный момент
бегущих волн. Форма первой из них в начальный момент ![]() имеет вид
имеет вид ![]() , а второй -
, а второй - ![]() . В сумме получаем
. В сумме получаем
![]() , чего и следовалоожидать.
, чего и следовалоожидать.
Чтобы наглядно представить себе картину процесса, для простоты будем считать, что ![]() четна и равна нулю всюду вне интервала
четна и равна нулю всюду вне интервала ![]() (рис. 8). Функция
(рис. 8). Функция ![]() в этом случае будет выглядеть так (см. рис. 8)
в этом случае будет выглядеть так (см. рис. 8)
На рисунке 9 показаны профили струны и графики ![]() и
и ![]() (пунктирные линии) в различные моменты времени.
(пунктирные линии) в различные моменты времени.
Как и в предыдущем случае,изобразим ход колебаний на фазовой плоскости (см. рис
10). Пользуясь выражением ( 19) для функции ![]() , получаем, что в зонах II, IV и VI отклонение обратной волны постоянно и равно
, получаем, что в зонах II, IV и VI отклонение обратной волны постоянно и равно ![]() , а в точках зон III,Vи VI такое же отклонение имеет прямая волна, поэтому зона VIпредставляет собой зону остаточного смещения, в точках, ейсоответствующих, функция
, а в точках зон III,Vи VI такое же отклонение имеет прямая волна, поэтому зона VIпредставляет собой зону остаточного смещения, в точках, ейсоответствующих, функция
![]() . В зоне IV прямая волна имеет отклонение
. В зоне IV прямая волна имеет отклонение
![]() , такое же отклонение в зоне Vимеет обратная волна. Поэтому обе этих зоны являются зонами покояточек струны.
, такое же отклонение в зоне Vимеет обратная волна. Поэтому обе этих зоны являются зонами покояточек струны.
| |
| |
| |
| Наверх | К началу | К оглавлению |
Метод характеристик
Для определения отклонения
Из формулы Даламбера ( 6) следует, что отклонение точки струны с координатой ![]() в момент времени
в момент времени ![]() определяется только значениями начального отклонения в вершинах
определяется только значениями начального отклонения в вершинах ![]() и
и
![]() характеристического треугольника и значениями начальной скорости частиц струны, расположенных на основании
характеристического треугольника и значениями начальной скорости частиц струны, расположенных на основании ![]() этого треугольника. Действительно, формула ( 6) при
этого треугольника. Действительно, формула ( 6) при ![]() и
и ![]() дает (такая запись не совсем корректна, зато весьманаглядна)
дает (такая запись не совсем корректна, зато весьманаглядна)
![$\displaystyle u(M_0)=\frac{1}{2}\left[\varphi(M_1)+\varphi(M_2)\right]+\frac{1}{2a}\int\limits_{M_1}^{M_2}\psi(\theta)\,d\theta.$](images/img239.png)
Это свойство решения задачи Коши ( 1),( 2)обусловлено конечной скоростью распространения возмущений впроцессах, описываемых волновым уравнением (уравнением гиперболического типа).
| Наверх | К началу | К оглавлению |
![\includegraphics[width=0.8\textwidth, height=0.3\textwidth, angle=0]{ris16.bmp}](images/img174.png)
![\includegraphics[width=0.5\textwidth, height=0.5466666\textwidth, angle=0]{ris4sam.bmp}](images/img181.png)
![\includegraphics[width=0.437999\textwidth, height=0.27\textwidth, angle=0]{ris17.bmp}](images/img182.png)
![\includegraphics[width=0.437999\textwidth, height=0.250284\textwidth, angle=0]{ris18.bmp}](images/img183.png)
![$\displaystyle u(x,t)=\frac{1}{2}\left[\varphi(x-at)+\varphi(x+at)\right].$](images/img198.png)
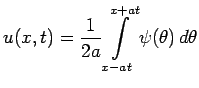
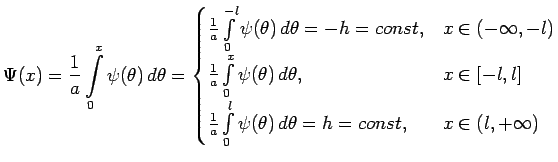
![\includegraphics[width=0.5533333\textwidth, height=0.3\textwidth, angle=0]{ris19.bmp}](images/img235.png)