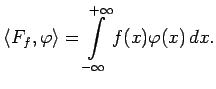Обобщенные решения уравнения колебаний
Физические задачи далеко не всегда приводят к начальным условиям, достаточно гладким для того, чтобы формула Даламбера давала классическое (дифференцируемое два раза) решение задачи (1), (2). В этом случае полезным оказывается понятие так называемого "обобщенного решения" уравнения (1). Различных определений обобщенного решения существует несколько. Мы рассмотрим три из них.
| Наверх | К началу | К оглавлению |
Определение обобщенных решений уравнения колебаний через интегральные тождества
Определение 2
Определение 3 Функция ![]() называется обобщенным решением
уравнения (1), если
называется обобщенным решением
уравнения (1), если
![$\displaystyle \forall\,\,\,\eta\in
A\,\,\,\exists\,\iint\limits_{\Omega_\eta}u(x,t)\left[\eta_{tt}(x,t)-a^2\eta_{xx}(x,t)\right]\,dxdt=0$](images/img73.png)
Покажем, что классические решения уравнения (1) удовлетворяют определению 3.
![]()
![]() - решение (1)
- решение (1)
![]()
![]() (13) выполняется.
(13) выполняется.
![]() Пусть
Пусть
![]() в какой-нибудь
точке
в какой-нибудь
точке ![]() .
.
![]() - дважды непрерывно
дифференцируемая функция
- дважды непрерывно
дифференцируемая функция
![]()
![]() -
непрерывная функция
-
непрерывная функция
![]()
![]() и
сохраняет знак в некоторой окрестности
и
сохраняет знак в некоторой окрестности ![]() точки
точки
![]() . Выберем функцию
. Выберем функцию
![]() . Для этой функции
(13), очевидно, не выполняется. Мы пришли к
противоречию, значит
. Для этой функции
(13), очевидно, не выполняется. Мы пришли к
противоречию, значит
![]()
![]()
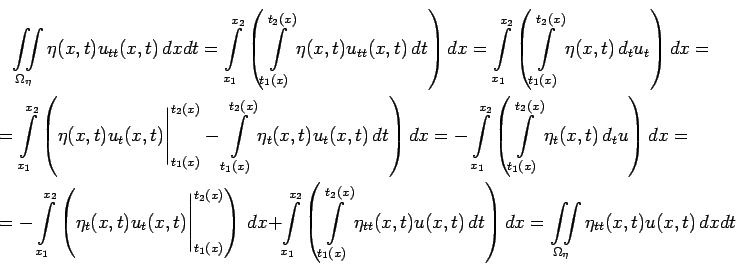
Аналогично можно показать, что
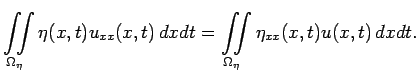
| Наверх | К началу | К оглавлению |
Обобщенные решения задачи Коши для уравнения колебаний, как предел последовательности классических решений
Определение 4 Функция |
таких что
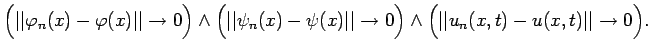
В качестве норм используются следующие (для функций двух и одной переменной соответственно):
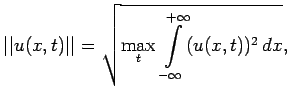
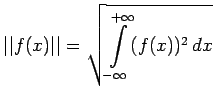
Предельная функция для последовательности
![]() уже не обязательно всюду
дифференцируема (см. рис. 1 а), а может быть
даже разрывна (см. рис. 1 б).
уже не обязательно всюду
дифференцируема (см. рис. 1 а), а может быть
даже разрывна (см. рис. 1 б).
Очевидно, что классические решения, если они существуют, являются обобщенными решениями задачи (1), (2) в смысле определения 4.
Такое понятие обобщенного решения неудобно тем, что оно
трудно проверяемо: чтобы убедиться, что некоторая функция ![]() является обобщенным решением нашей задачи необходимо построить
последовательность гладких решений, сходящихся к ней.
является обобщенным решением нашей задачи необходимо построить
последовательность гладких решений, сходящихся к ней.
| Наверх | К началу | К оглавлению |
Определение обобщенных решений задачи Коши для уравнения колебаний с использованием обобщенных функций
Определения
Определение 5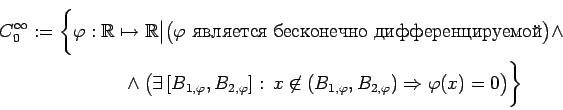
Определение 6Введем в
![]() метрику следующим образом: пусть
метрику следующим образом: пусть
![]() и
и ![]() - отрезок,
вне которого обе эти функции обращаются в нуль,
тогда
- отрезок,
вне которого обе эти функции обращаются в нуль,
тогда
- Функции из
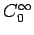 являются непрерывными, поэтому максимум в
(15) существует, значит
являются непрерывными, поэтому максимум в
(15) существует, значит
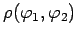 определена на всем
определена на всем
 .
.
-
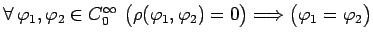 - очевидно
- очевидно
-
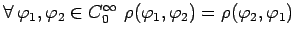 - очевидно
- очевидно
- Неравенство треугольника:
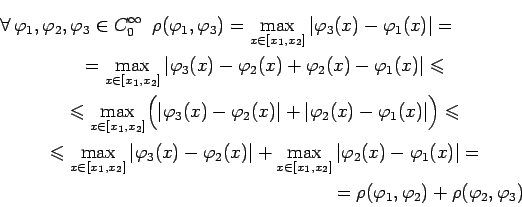
Определение 7 Под сходимостью последовательности функций
![]() к некоторой
к некоторой
![]() будем понимать одновременное
выполнение следующих двух условий:
будем понимать одновременное
выполнение следующих двух условий:
Определение 8Обобщенной функцией называется непрерывный линейный
функционал
![]() .
.
Здесь непрерывность функционала понимается в том смысле, что
Множество
обобщенных функций будем обозначать
![]() .
.
Значение обобщенной функции ![]() на функции
на функции
![]() будем обозначать
будем обозначать
![]() или
или
![]() .
Запись
.
Запись ![]() , хотя она и не совсем корректна, подчеркивает некоторую аналогию между обобщенными
функциями
и функциями действительного переменного, к тому же она пригодится
нам для определения операции "сдвинутой" обобщенной
функции
, хотя она и не совсем корректна, подчеркивает некоторую аналогию между обобщенными
функциями
и функциями действительного переменного, к тому же она пригодится
нам для определения операции "сдвинутой" обобщенной
функции
![]() .
.
Определение 9Будем называть обычными функции, интегрируемые на любом конечном интервале (в частности, непрерывные функции,очевидно, являются обычными).
Покажем, что любой обычной функции ![]() можно однозначно
поставить в соответствие некоторую обобщенную функцию по
формуле
можно однозначно
поставить в соответствие некоторую обобщенную функцию по
формуле
Линейность (16) очевидна. Докажем непрерывность этого функционала.
![]() Действительно, пусть последовательность
Действительно, пусть последовательность
![]() функций из
функций из
![]() сходится к некоторой функции
сходится к некоторой функции
![]() в смысле определения 7. Обозначим
в смысле определения 7. Обозначим
![]() - интервал, вне которого функции
- интервал, вне которого функции ![]() обращаются в нуль (он существует по определению 7).
обращаются в нуль (он существует по определению 7).
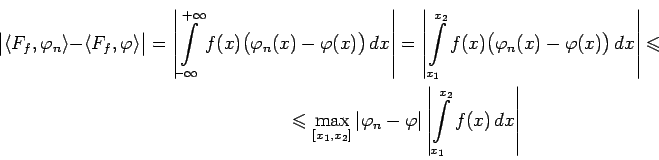
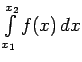 равен некоторой константе, значит
равен некоторой константе, значит
![$ \max\limits_{[x_1,x_2]}\vert\varphi_n-\varphi\vert\left\vert\int\limits_{x_1}^{x_2}f(x)\,dx\right\vert\xrightarrow[n\rightarrow\infty]{}0$](images/img130.png) ,
а отсюда следует
,
а отсюда следует
![]()
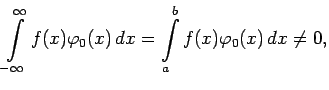
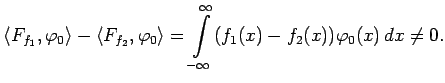
Можно доказать также и более общее утверждение: если двум функциям
![]() и
и ![]() , интегрируемым на любом конечном отрезке,
соответствует одна и та же обобщенная функция
, интегрируемым на любом конечном отрезке,
соответствует одна и та же обобщенная функция ![]() , то эти функции
совпадают везде, за исключением множества меры нуль.
, то эти функции
совпадают везде, за исключением множества меры нуль.
| Наверх | К началу | К оглавлению |
Операции над обобщенными функциями
Определение 10Произведение
![]() функции
функции
![]() на
на
![]() определим так
определим так
Определение 11Сдвинутую на число ![]() функцию
функцию
![]() будем обозначать
будем обозначать ![]() и зададим следующим образом
и зададим следующим образом
Определение 12Производная
![]() от обобщенной функции
от обобщенной функции
![]() определяется следующей формулой
определяется следующей формулой
Замечательной особенностью обобщенных функций является
существование их производных любого порядка (это обусловлено тем,
что функции
![]() бесконечно дифференцируемы). Теперь,
даже если какая-то обычная функция не является дифференцируемой,
мы всегда можем найти производные любого порядка для
соответствующей ей обобщенной функции. На этом факте и основано
третье определение обобщенного решения.
бесконечно дифференцируемы). Теперь,
даже если какая-то обычная функция не является дифференцируемой,
мы всегда можем найти производные любого порядка для
соответствующей ей обобщенной функции. На этом факте и основано
третье определение обобщенного решения.
| Наверх | К началу | К оглавлению |
Примеры обобщенных функций
Для нас будут важны две обобщенные функции.
Функция Дирака ![]() определяется так:
определяется так:
Функция Хевисайда ![]()
Функция Хевисайда - обобщенная функция, соответствующая
обычной функции
![$\displaystyle H(x)=\begin{cases}
0,&x\in[-\infty,0)\\
1,&x\in[0,+\infty]
\end{cases}$](images/img154.png)
Легко убедиться, что
![]() :
:
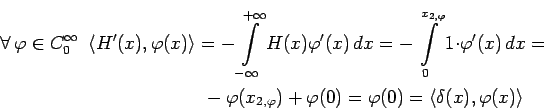
| Наверх | К началу | К оглавлению |
Нахождение обобщенных решений
Прежде всего, отметим, что обобщенные частные производные от функции двух переменных
Определение 13Обобщенным решением задачи (1), (2)
называется функция ![]() , такая, что (1), (2) обращаются в тождества при
подстановке этой функции в них, если под производными
, такая, что (1), (2) обращаются в тождества при
подстановке этой функции в них, если под производными ![]() понимать ее обобщенные производные.
понимать ее обобщенные производные.
В качестве примера рассмотрим задачу (1), (2) при
По формуле Даламбера (6) получаем
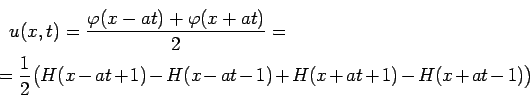
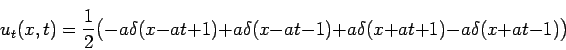
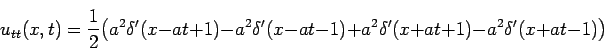
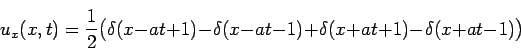
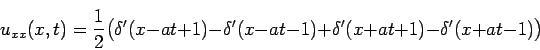
Видим, что полученная по формуле Даламбера функция
Аналогично можно получить решение для любых кусочно
непрерывных
![]() и
и ![]()
| Наверх | К началу | К оглавлению |
![$\displaystyle \forall\,\,\,\eta\in A\,\,\,\exists\,\iint\limits_{\Omega_\eta}\eta(x,t)\left[u_{tt}(x,t)-a^2u_{xx}(x,t)\right]\,dxdt=0$](images/img74.png)
![\includegraphics[width=0.8\textwidth, height=0.3409594\textwidth, angle=0]{ris10.bmp}](images/img97.png)