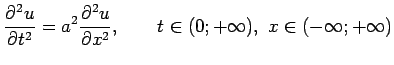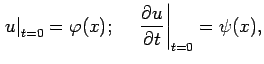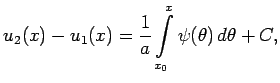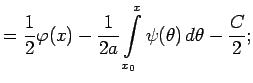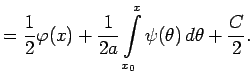Задача Коши для волнового уравнения и ее решение
Физический смысл задачи
Рассмотрим свободные колебания бесконечной струны, т.е. настолько длинной, что влиянием ее концов на процесс колебаний можно пренебречь. Причинами колебаний могут являться начальные отклонения струны от равновесного положения и (или) сообщенный струне начальный импульс, обуславливающий некоторое начальное распределение скоростей частиц струны.
| Наверх | К началу | К оглавлению |
Математическая постановка задачи
Нужно решить однородное уравнение колебаний
при начальных условиях
где функции
Задача (1), (2) называется задачей Коши для волнового уравнения.
| Наверх | К началу | К оглавлению |
Решение
![]() Введем новые переменные
Введем новые переменные
эта замена является невырожденной:
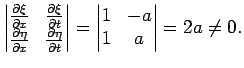 |
Преобразуя производные к новым переменным, находим:
Уравнение (1) в новых переменных запишется слудующим образом:
| (4) |
Общий вид решения этого уравнения мы можем найти интегрированием:
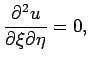 |
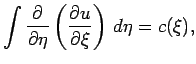 |
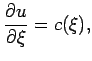 |
где
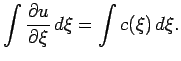 |
Пусть
где
Следовательно, функция вида
| (5) |
удовлетворяет уравнению (1).
![]() По теореме 1 решение (1) имеет вид
По теореме 1 решение (1) имеет вид
Интегрируя (8) в пределах от ![]() (константа) до
(константа) до ![]() получаем
получаем
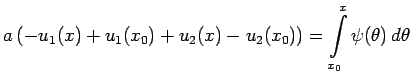 |
Пусть
Из системы уравнений (7), (9) имеем
Подставляя (10) и (11) в (3), находим
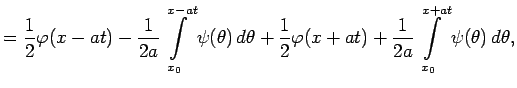 |
||
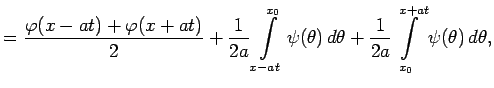 |
или
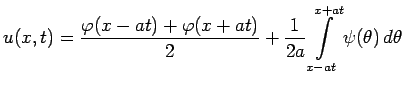 |
(12) |
Определение 1Формула (6) называется формулой Даламбера.
| Наверх | К началу | К оглавлению |
Существование и единственность решения
Таким образом, если
![]() дифференцируема 2 раза, а
дифференцируема 2 раза, а
![]() дифференцируема, то решение задачи Коши
существует и единственно.
дифференцируема, то решение задачи Коши
существует и единственно.
| Наверх | К началу | К оглавлению |
Непрерывная зависимость решения от начальных условий
Докажем, что решение задачи Коши для волнового уравнения меняется непрерывно при непрерывном изменении начальных условий.
![$\displaystyle \Bigl((\vert\varphi_1(x)-\varphi_2(x)\vert<\delta)\wedge(\vert\ps...
...igl(\forall\,\, t\in[0;t_0]\,\, \vert u_1(x,t)-u_2(x,t)\vert<\varepsilon\bigr),$](images/img57.png) |
где
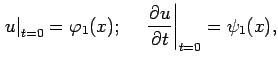
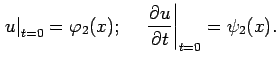
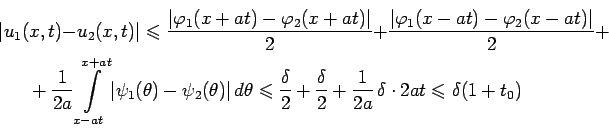
При
| Наверх | К началу | К оглавлению |