Московский Государственный Строительный Университет Арефьев В.Н. Лекции по "Уравнениям математической физики"

Лекция 3. Метод Фурье

Метод Фурье - один из распространенных и эффективных методов решения уравнений с частными производными. Этот метод часто встречается и под другими названиями: метод разделения переменных или метод собственных функций.

Общая схема метода Фурье.

Основная идея этого метода состоит в том, что решение задачи для уравнения с частными производными сводится к решению вспомогательных задач для уравнений с меньшим числом независимых переменных. В частности, если заданное уравнение содержит две независимые переменные, то вспомогательные задачи будут уже зависеть только от одной переменной. Таким образом решение уравнения с частными производными сводится к решению обыкновенных дифференциальных уравнений.

При применении метода Фурье удобно использовать следующую лемму.

Основная лемма метода Фурье.

Если в прямоугольнике R плоскости XOY:

для некоторых функций выполняется тождество



то в этом случае

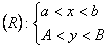
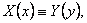
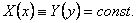
Доказательство. Предположим противное, т.е. что

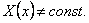
Тогда существуют значения такие, что

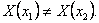
Рассмотрим точки (x₁,y) и (x₂,y), принадлежащие прямоугольнику R. На R справедливо тождество (8), а поэтому

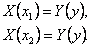
Сравнивая эти равенства, приходим к противоречию с нашим предположением. Следовательно X(x) = const, а тогда Y(y)=const.

Решение первой начально-краевой задачи для волнового уравнения.

Рассмотрим волновое уравнение

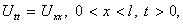
Граничные условия первого рода

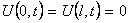
И начальные условия

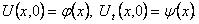
Решим эту задачу методом Фурье.

Шаг 1. Представим функцию U(x,t) в виде

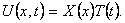
Найдем частные производные U_xx и U_tt и подставим в уравнение (9):

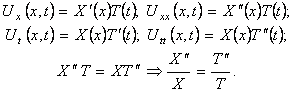
В полученном уравнении левая часть зависит только от x, а правая- только от t. Используя основную лемму, заключаем:

тогда

Из граничных условий (10) получим

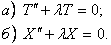
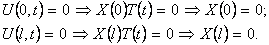
Шаг 2. Решим задачу Штурма-Лиувилля

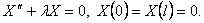
Она имеет собственные значения и собственные функции

Шаг 3. Подставим найденные значения λ_n в уравнение а) и решим его:

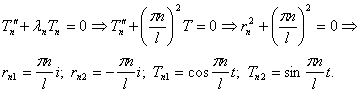
Шаг 4. Выпишем частные решения уравнения (9):

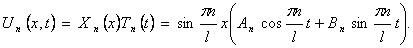
Для волнового уравнения эти решения называются собственными колебаниями. В лекции 6 мы изучим их подробнее. В силу линейности и однородности уравнения (9) линейная комбинация этих решений

также будет решением этого уравнения, причем функция U(x,t) удолетворяет заданным граничным условиям (10).

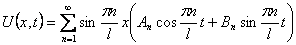
Замечание 1. Здесь мы предполагаем, что полученный функциональный ряд равномерно сходится и его можно дважды почленно дифференцировать по x и по t в области 0<x<l, t>0. Об условиях, при которых это можно сделать, будет рассказано в лекции 5.

Шаг 5. Определим коэффициенты A_nи B_n в формуле (12), используя начальные условия (11). Из первого начального условия получим

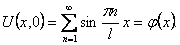
Равенство (13) означает, что начальная функция φ(x) разлагается в ряд Фурье по синусам, которые в данном случае являются собственными функциями X_n(x) задачи Штурма-Лиувилля.

Коэффициенты Фурье вычисляются по формулам

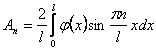
Из второго начального условия находятся коэффициенты B_n.

Отсюда B_n равны

Вычислив коэффициенты A_n и B_n для конкретных начальных функций и подставив их значения в (12), мы получим решение первой начально-краевой задачи.

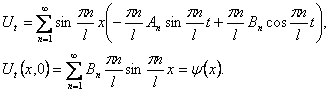
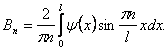
Замечание 2. Используя формулу (12), можно получить решение первой начально-краевой задачи для уравнения колебания струны: Для этого проведем замену переменной τ=at и получим

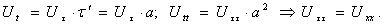
При этом начальное условие не изменится, а условие преобразуется к виду Тогда решение задачи в переменных (x,τ) будет иметь вид

где

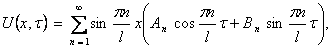
Возвращаясь к переменным (x,t), получим

где

Хостинг от uCoz