Лекция 12. Ряды Фурье

Ряд Фурье является частным случаем функциональных рядов. Функциональным рядом называется выражение вида

где U₁(x),U₂(x), ... ,U_k(x), ... - функции, зависящие от одной переменной х или от нескольких переменных (тогда через х обозначают точку в пространстве: х = (х₁, ... , x_n)). В прикладных задачах часто возникает необходимость рассматривать функции двух и трёх переменных. В этой лекции мы будем рассматривать только случай одной переменной. Общий случай можно изучать по учебной литературе. Пусть функции U_k(x), k=1,2,... определены в некотором интервале оси ОХ. При каждом фиксированном значении х=x₀ из этого интервала функциональный ряд превращается в числовой ряд

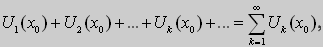
который может сходится, а может и расходится. В первом случае точка x = x₀ называется точкой сходимости функционального ряда. Множество всех точек сходимости называется областью сходимости ряда. В базовом курсе математики рассматриваются степенные ряды

Областью сходимости такого ряда является либо одна точка x = x₀, либо интервал радиуса R с центром в точке x₀ : (x₀-R,x₀+R), включая иногда один или два конца, либо вся прямая Отыскание области сходимости функционального ряда (в общем случае) представляет трудную задачу.

В теории тригонометрических рядов рассматриваются ортогональные системы функций. Две функции φ(x) и ψ(x) называются ортогональными на отрезке[a,b] (или в интервале (a,b)),если

При этом предполагается, что

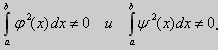Система функций {φ_n(x),n=0,1,2, ... }- ортогональна на отрезке [a,b] (или в интервале (а,b)),если

Здесь тоже предполагается, что

Иными словами,система функций {φ_n(x), n = 0, 1, 2, ...} ортогональна на отрезке [a,b], если все функции попарно ортогональны. Число

называется нормой функции φ_n(x). Если все функции φ_n(x) имеют единичную норму и система ортогональна на [a,b], то такая система функций называется ортонормированной.

Простейшим примером ортогональной системы функций служит тригонометрическая система

{1, sinx, cosx, sin 2x, cos 2x, ... , sin nx, cos nx, ...}

(52)

на отрезке [-π, +π]. Чтобы убедиться в этом, надо вычислить следующие интегралы:

1. . Поэтому

Если n=m, то .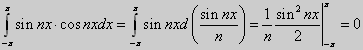

Аналогично вычисляются и другие интегралы:

при n ≠ m, n, m = 1, 2, 3, ... Если n = m, то

Значит,

при n ≠ m, n, m = 1, 2, 3, ... Если n = m, то

То есть

Таким образом, доказано, что система (52) на отрезке [ - π, + π] ортогональная, но не ортонормированная. Если функции в системе (1) нормировать, то есть взять систему

то такая система функций будет ортонормированной. Приведём ещё примеры ортогональных систем:

          1) {1,cosx,cos2x, ... ,cosnx, ...} на отрезке [0, π],
          2) {sinx,sin2x, ... ,sinnx, ...} на отрезке [0, π],

          3)

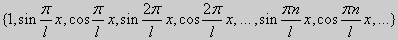на отрезке [-l, l],

4) на отрезке [0, l],

5) на отрезке [0, l],

Тригонометрическим рядом Фурье функции f(x), имеющей период T = 2l, называется ряд вида

(53)

в котором коэффициенты a_o, a_n, b_n вычисляются по формулам

,	n = 1, 2, 3, ...

При этом говорят, что ряд (53) порождён функцией f(x), а коэффициенты a_o, a_n, b_n называются коэффициентами Фурье. В случае, когда функция f(x) имеет период Т = 2π, её ряд Фурье имеет вид

и коэффициенты Фурье вычисляются по формулам

Для четных функций ряд Фурье (53) содержит только члены

для нечетных функции - только члены В этих случаях коэффициенты Фурье удобнее вычислять по формулам

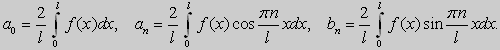
Важное значение имеют вопросы о том, при каких х ряд Фурье сходится и в каком случае сумма ряда в точке х равна значению функции f(x), порождающей этот ряд. Ответ на эти вопросы дает теорема Дирихле.

Функция f(x) на отрезке [а, b] удовлетворяет условиям Дирихле, если
a) f(x) на отрезке [а, b] непрерывна или имеет на этом отрезке конечное число точек разрыва I рода;
b) в каждом интервале непрерывности f(x) монотонна, либо имеет на этом интервале конечное число точек экстремума.

Например, функция, изображенная на рис. 22, удовлетворяет условиям Дирихле.

Рис.22

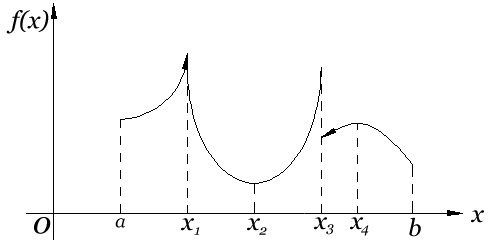
Теорема Дирихле. Функция f(x), периодическая с периодом Т = 2l, удовлетворяющая условиям Дирихле на отрезке [-l,l], разлагается в тригонометрический ряд Фурье (53), причем:
a) в каждой точке непрерывности х функции f(x) ряд Фурье (53) сходится к значению f(x);
b) в каждой точке разрыва х_i, функции f(x) ряд Фурье (53) сходится к значению

Тригонометрический ряд Фурье является частным случаем рядов, которые получаются для произвольных систем функций, ортогональных на отрезке [а, b]. Причем сами функции не обязаны быть периодическими.

Рассмотрим систему функций {φ_n(x), n = 0, 1,2,...}, ортогональную на отрезке [а, b].Рядом Фурье функции f(x) по ортогональной системе функции{φ_n(x)} называется ряд видa

в котором коэффициенты Фурье C_n вычисляются по формулам

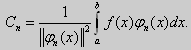
Если система функций {φ_n(x), n = 0, 1, 2, ...} ортонормированная, то коэффициенты Фурье равны

Вопрос о сходимости этих рядов Фурье изучается в специальной научной литературе. Один из результатов сформулирован в теореме Стеклова(Дополнительные вопросы, лекция 4).

Теперь вернемся к тригонометрическим системам функций

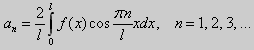
на отрезке [0, l]. Функцию f(x) будем также рассматривать только на отрезке [0, l].Тогда ряд

называется рядом Фурье функции f(x) по косинусам, если коэффициенты вычисляются по формулам:

Аналогично, ряд

называется рядом Фурье функции f(x) по синусам, если коэффициенты вычисляются по формуле

, n = 1, 2, 3, ...

Относительно сходимости этих рядов справедлива теорема, аналогичная теореме Дирихле. А именно, если функция f(x) удовлетворяет на отрезке [0, l] условиям Дирихле, то ряд по косинусам и ряд по синусам сходятся. Причем в тех точках, где f(x) непрерывна, суммы рядов равны значению функции. В точках разрыва функции f(x) суммы рядов равны среднему арифметическому значений левостороннего и правостороннего пределов. На концах отрезка сумма ряда по косинусам совпадает со значениями функции, а сумма ряда по синусам равна нулю.