Лекция 1. Введение

Будем рассматривать функции вида U=U(x₁,x₂,…,x_n), x=(x₁,x₂,...,x_n) .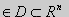

В частных случаях:

при n=2: x₁= x; x₂= y => U=U(x,y) либо x₁= x; x₂= t => U=U(x,t);

при n=3: x₁ = x; x₂ = y; x₃ = z => U=U(x,y,z) либо x₁= x; x₂= y; x₃= t => U=U(x,y,t);

при n=4: x₁ = x; x₂= y; x₃ = z;x₄ = t => U=U(x,y,z,t).

В этом случае переменные x, y, z называются пространственными переменными, t - время.

Условимся для простоты записи обознать частные производные 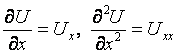, и т.д.

Определение. Дифференциальным уравнением с частными производными называется уравнение вида

Другими словами - это уравнение, связывающее независимые переменные x_i, неизвестную функцию U и ее частные производные до порядка k.

Определение. Порядком дифференциального уравнения с частными производными называется высший из порядков частных производных, входящих в это уравнение.

Определение. Решением уравнения с частными производными порядка k называется функция U=U(x₁, x₂ , … ,x_n), определенная в некоторой области 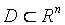, которая имеет производные до порядка k и при подстановке в уравнение обращает его в тождество по (x₁, x₂, … , x_n).

Определение. Дифференциальное уравнение с частными производными называется линейным, если функция U и ее частные производные входят в него линейным образом.

Запишем общий вид линейного уравнения с двумя переменными:

в случае уравнения 1-го порядка:

(1)

в случае уравнения 2-го порядка:

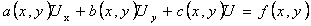
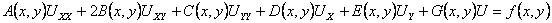
(2)

Функции a(x, y), b(x, y), … , A(x, y), B(x, y) … - коэффициенты (заданные функции), f(x, y)- правая часть (заданная функция) линейного дифференциального уравнения.

Определение. Дифференциальное уравнение с частными производными называется однородным, если его правая часть тождественно равна нулю, т.е 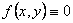при всех (x,y)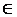D.

Определение. Дифференциальное уравнение с частными производными называется неоднородными, если его правая часть тождественно не равна нулю, т.е. 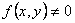при некоторых (x,y)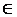D.

Определение. Если коэффициенты линейного дифференциального уравнения - постоянные, то такое уравнение называется линейным дифференциальным уравнением с постоянными коэффициентами.

Левая часть уравнения (1) или (2) обычно обозначается через LU и называется линейным дифференциальным оператором с частными производными порядка 1 или 2, соответственно. Тогда линейное неоднородное дифференциальное уравнение будет иметь вид LU = f(x ,y), а линейное однородное дифференциальное уравнение будет иметь вид LU = 0.

Определение. Выражение вида 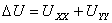или 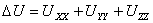называется оператором Лапласа, соответственно, на плоскости или в пространстве.

Условимся для более краткой записи сокращать (линейное) дифференциальное уравнение до (Л)ДУ, линейное (не)однородное дифференциальное уравнение до ЛОДУ (ЛНДУ).

Среди ЛДУ второго порядка есть уравнения, которые имеют особое значение. Перечислим их:

1. Уравнение Лапласа- уравнение вида ∆U=0 (n=2,3)- ЛОДУ 2-го порядка.

Уравнение Пуассона- уравнение вида ∆U=f (n=2,3)- ЛНДУ 2-го порядка.

2. Волновое уравнение- уравнение вида U_tt=a²ΔU, где ΔU=U_xx+U_yy на плоскости или ΔU=U_xx+U_yy+U_zz в пространстве. Одномерное волновое уравнение (на прямой)- уравнение вида U_tt=a²U_xx.

3. Уравнение теплопроводности- уравнение вида U_t=a²∆U, где где ΔU=U_xx+U_yy на плоскости или ΔU=U_xx+U_yy+U_zz в пространстве. Одномерное уравнение теплопроводности (на прямой)- уравнение вида U_t=a²U_xx.

Именно эти уравнения являются основными уравнениями математической физики.

Основные свойства решений ЛДУ (в том числе обыкновенных).

1.Линейность: если U₁ и U₂- решения ЛОДУ, k₁ и k₂ - постоянные, то k₁U₁+k₂U₂тоже решение ЛОДУ L(k₁U₁+k₂U₂)=0.

2. Если U₁ и U₂ - решения ЛНДУ LU=f, то (U₁-U₂) - решение ЛОДУ LU=0, соответствующего данному ЛНДУ.

3. Принцип суперпозиции решений: если U₁ и U₂ - решенияЛНДУ LU₁=f₁ и LU₂=f₂соответственно, то (U₁+U₂)- решение ЛНДУ L(U₁+U₂)=f₁+f₂.

Кроме этих свойств решения ДУ с частными производными могут обладать некоторыми "особыми" свойствами.
4. ДУ с частными производными могут иметь бесконечное множество линейно независимых решений. Из этих решений можно составить ряд с произвольными коэффициентами. Тогда, если ряд сходится и его можно почленно дифференцировать необходимое число раз, то он также является решением ДУ.

Пример.

Рассмотрим функции двух переменных U_n=sinnxcosny. Из теории тригонометрических рядов следует, что система функций {U_n} ортогональна в области [-π,π]x[-π,π] и, следовательно, линейно независимая. Нетрудно проверить, что они являются частными решениями ДУ U_xx=U_yy. Пусть ряд 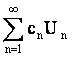сходится и его можно дважды почленно дифференцировать. Тогда функция 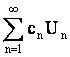также является решением ДУ U_xx = U_yy.

5. Решениями ДУ с частными производными могут быть любые функции (при условии, что они имеют соответствующие частные производные).

Пример.

Возьмем уравнение U_xy = 0 и решим его. Для этого первый раз будем интегрировать по x (считая y постоянной величиной):

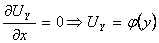- произвольная функция.

Полученное равенство проинтегрируем еще раз, теперь уже по y, считая x постоянной величиной:

,

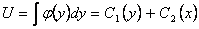где C₁(y) - первообразная от произвольной функции φ(y) и потому также произвольная (дифференцируемая) функция. Таким образом, общее решение уравнения U_xy=0 зависит от двух произвольных функций.

Классификация дифференциальных уравнений с частными производными.

Уравнения с частными производными можно классифицировать по разным признакам.

Например:

1. По порядку уравнений: U_t=U_xx (уравнение 2-го порядка), U_t=U_x(уравнение 1-го порядка), U_t=U_xxx + sinx (уравнение третьего порядка).

2. По числу независимых переменных: U_t=U_xx (уравнение с 2-мя переменными), - уравнение с тремя переменными.

3. ДУ с частными производными могут быть линейными и нелинейными. Линейные уравнения в свою очередь бывают однородными и неоднородными.

4. ЛДУ 2-го порядка классифицируются по типу:

а) Гиперболический тип ( в области D), если выражение δ(x,y)=B²-AC>0 для любых (x, y)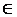D, где A, B, C - коэффициенты в уравнении (2)

б) Эллиптический тип (в области D), если выражение δ(x,y)=B²-AC<0 для любых (x,y) 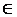D

в) Параболический тип (в области D), если выражение δ(x,y)=B²-AC = 0 для любых (x,y)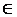D.

Отметим, что тип уравнения определяется только коэффициентами A,B,C при производных 2-го порядка. При невырожденной замене переменных тип не меняется.

г) Смешанный тип, если в области D уравнение имеет разный тип в разных точках.

Пример. Рассмотрим уравнение

yU_xx + U_yy = 0
Оно возникает в газовой динамике и называется уравнением Трикоми. Для этого уравнения выражение δ(x,y) = B² - AC = -y. Тогда при y>0 выражение δ(x,y)<0 и уравнение имеет эллиптический тип. При y<0 выражение δ(x,y)>0, следовательно, уравнение гиперболического типа, а при y=0, соответсвенно, δ(x,y)=0 и уравнение имеет параболический тип (см. рис. 1)

Рис. 1

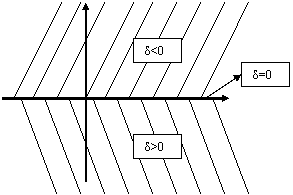
Замечания.
1. Уравнения с постоянными коэффициентами имеют один тип на всей области определения. Так, например, волновое уравнение на плоскости и в пространстве имеет гиперболический тип, уравнение теплопроводности на плоскости и в пространстве - параболический тип, а уравнение Лапласа - эллиптический тип.

2. Классификация ЛДУ с большим числом переменных почти аналогична.

Канонический вид ЛДУ 2-го порядка с частными производными (n=2).

В случае двух переменных существует невырожденная замена переменных ξ=ξ(x,y), η=η(x,y) (где ξ(x,y), η(x,y) дважды непрерывно дифференцируемые функции и якобиан 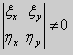такая, что уравнение (2) приводится к одному из следующих видов:

1. U_ξξ-U_ηη=f(ξ,η,U,U_ξ,U_η) (гиперболический тип).

2. U_ξξ+U_ηη=f(ξ,η,U,U_ξ,U_η) (эллиптический тип).

3. Uηη=f(ξ,η,U,U_ξ,U_η) (параболический тип).

Определение. Уравнения вида 1-3 называются каноническими уравнениями.

В соответствии с этим определением одномерное волновое уравнение и уравнение теплопроводности при a=1 имеют канонический вид.

Для уравнений с постоянными коэффициентами всегда существует линейная замена переменных ξ=ax+by, η=cx+dy, с помощью которой уравнение можно привести к каноническому виду.

Замечание. В случае n>2 переменных уравнение второго порядка всегда можно привести к каноническому виду в любой точке, однако в области это не всегда можно сделать.

Зачем нужно классифицировать и приводить уравнения к каноническому виду?

Типом уравнения определяются основные свойства решений.
Три типа уравнений соответствуют трем видам физических процессов- волновым, диффузионным и стационарным.

Волновые процессы: колебания сред, сооружений, электрические, звуковые, электромагнитные колебания.

Диффузионные процессы: тепломассоперенос (температура,диффузия газов).

Стационарные процессы:стационарное распределение температуры, установившиеся колебания сред, задачи дифракции, потенциальное течение жидкости, электростатический потенциал.

Канонические уравнения хорошо изучены. Уравнение общего вида сводится к каноническому, которое хорошо изучено. Часто можно найти его решение аналитически и вернуться к прежним переменным.
Для канонических уравнений разработанны численные методы решения.